Der zweite, etwas kniffligere Teil ist die Frage, ob dieser Punkt in einem Dreieck liegt. Wenn eine Ebene durch drei Punkte A,C und S gegeben ist, dann benutzen wir z.B. die Parameterdarstellung \(\overrightarrow {OA}+r \cdot \overrightarrow {AS}+s \cdot \overrightarrow {AC}\).
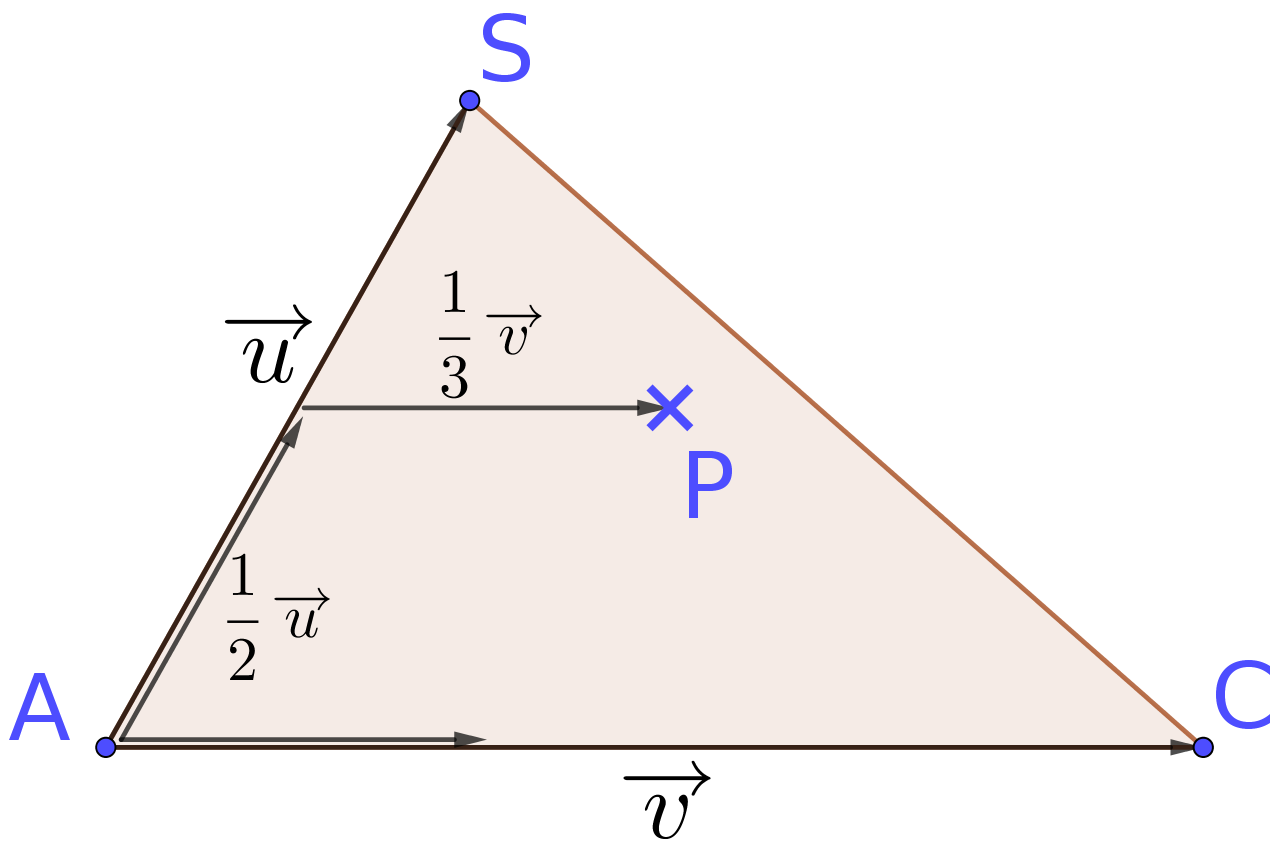
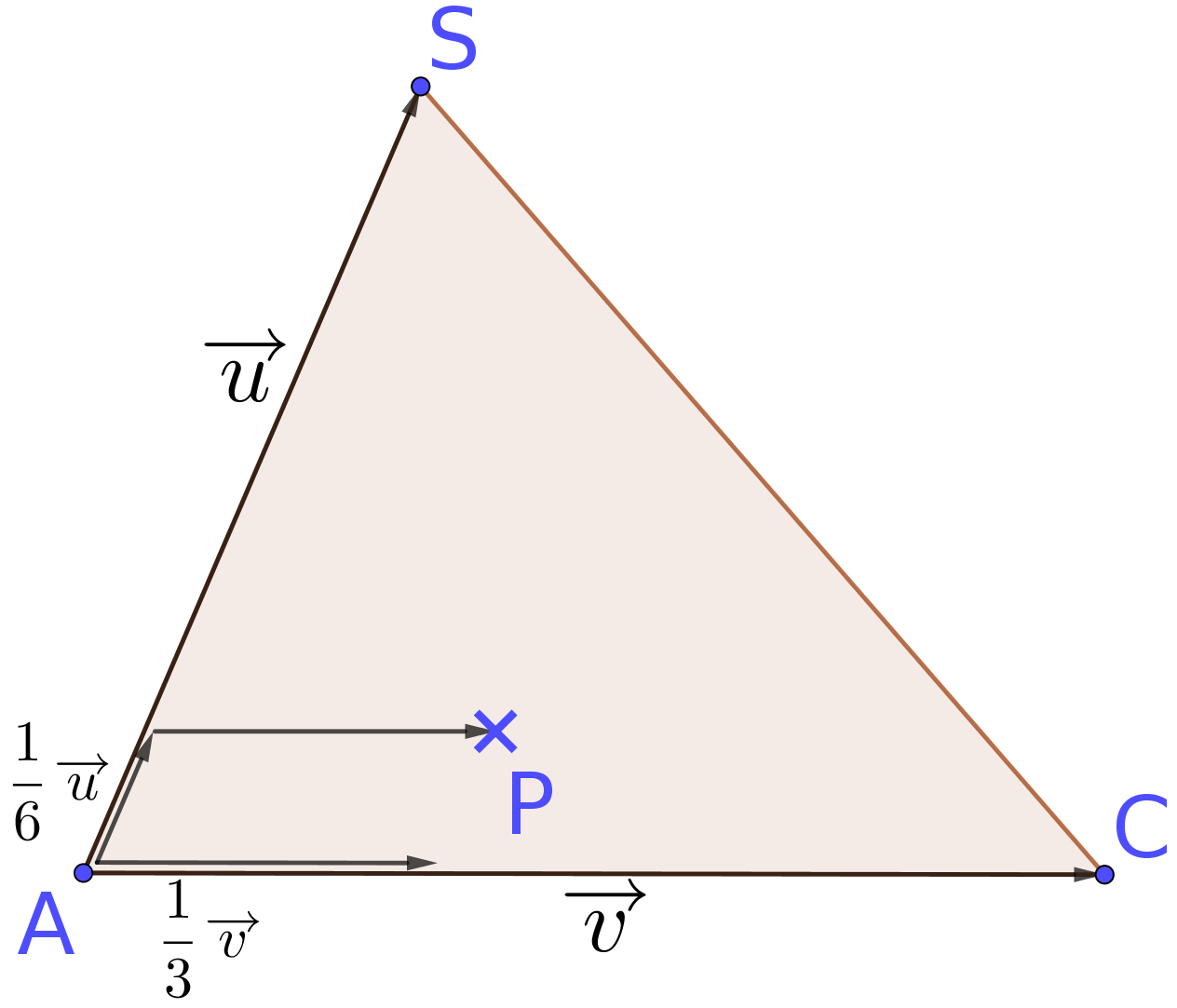
In der Skizze rechts wurde die Situation mit \(\vec u=\overrightarrow {AS}\) und \(\vec v=\overrightarrow {AC}\) ohne den Stürzvektor gezeichnet. Dazu wurden die Vektoren \({1 \over 2} \vec v\) und \({1 \over 3} \vec u\), sowie deren Summe angedeutet. Man kann sich jetzt mit den Strahlensätzen überlegen, dass der Punkt P im Inneren des Dreiecks liegen muss, solange die Faktoren zwischen 0 und 1 liegen und die Summe der Faktoren (also hier \({1 \over 2}+{1 \over 3}\) ) kleiner als 1 ist. Diese Überlegung ist sicher im AFB III, also der schwierigste Teil der Aufgabe. Allerdings gehört zu einer Klausur auch ein Aufgabenteil, in dem ihr eure Fähigkeiten in eine komplett neue Fragestellung übersetzen müsst, wie in dieser Aufgabe - diese dient dazu, die sehr guten SuS in die Kategorien 13/14/15 abzustufen. Keine Panik, wenn die (noch) nicht klappt :) Und: Wenn ihr Überlegungen mathematisch formuliert, die zielführend aber nicht perfekt sind, gibt es sicher Teilpunkte.