Bei Grenzprozessen kommen oft iterativ definierte Funktionen vor, wie etwa im Buch auf Seite 200 Nr. 12. Am einfachsten kann man diese mit der ans Funktion des GTR lösen (ans erreicht man mit ctrl (–) ).
Zum Beispiel Nr. 12 (1): \[x_n=0,6x_{n-1}+3\mbox{; }x_0=1.\] Der Anfangswert ist \(x_0=1\), also tippt man:
1enter Antwort:1Und jetzt einfach enter mehrmals:
enterenterenterenter
Antwort:5.16
6.096
6.6576
6.99456
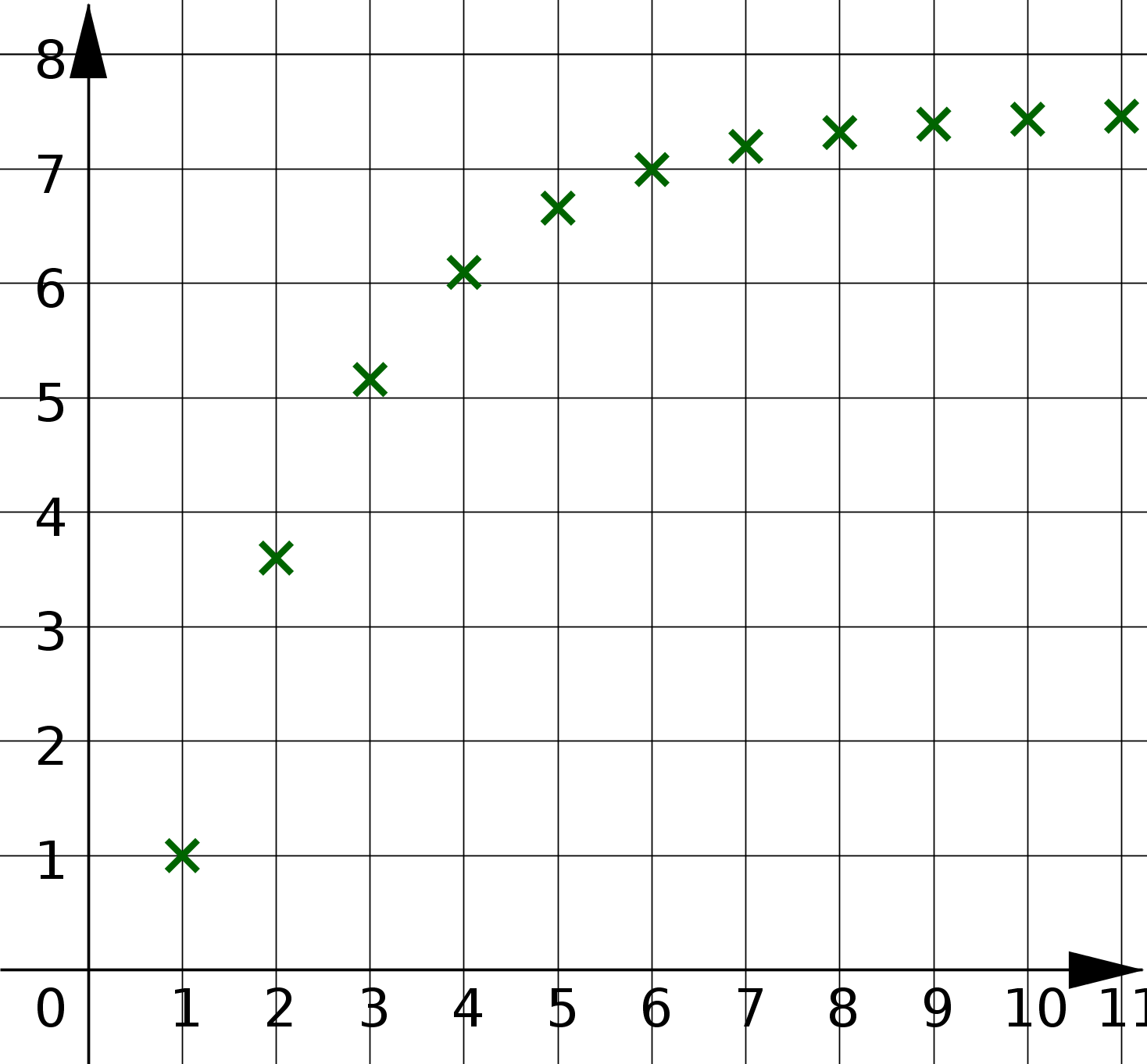
| Durch häufiges Drücken von Enter findet man heraus, dass die Zahlen sich immer mehr dem Wert 7,5 nähern (Bild rechts). | |
Manchmal genügtansnicht. Entweder, weil in der Definition nicht nur \(x_{n-1}\), sondern auch \(n\) vorkommt, oder weil man eine Grafik haben möchte. Dann gibt es zwei Möglichkeiten:
Öffne ein Grafik Fenster (z.B. B im Hauptmenu ). Dann:
| Für die Folge oben ist der Anfangswert 1 und die Funktion ist \(x_n=0,6x_{n-1}+3\mbox{; }x_0=1.\) oder in GTR-Schreibweise:\(u1(n)=0,6u1(n-1)+3\); Anfangswert=1 und Beginn bei n=0. Wenn man alles perfekt machen wollte, wäre das: | Dritte Zeile 0≤n um die Folge bei 0 anfangen zu lassen, meist nicht so wichtig) |
 |
Wenn es nicht im Grafikmenu sein soll, kann man eine Folge mit der Taste definieren. Nehmen wir als Beispiel wieder die harmonische Reihe aus der Aufgabe 14 mit \[x_n=x_{n-1}+\frac 1 n \mbox{ ; und } x_1=1.\] Zuerst ins Hauptmenu, dann A. Jetzt f(n):= und dann die Taste . Hier in der oberen Reihe an der siebten Stelle die \(\left\{{\square,\square}\atop{\square,\square}\right.\) wählen. Die beiden Bedingungen sind: Für \(n=1\) ist \(x_n=x_1=1\) und sonst ist \(x_n=x_{n-1}+\frac 1 n\). Also gib es so ein:
|
\(f(n):=\left\{\begin{matrix} 1 & , & n=1 \\ f(n-1)+\frac 1 n & , & \end{matrix} \right.\)
| was der GTR ergänzt zu: |
\(f(n):=\left\{\begin{matrix} 1 & , & n=1 \\ f(n-1)+\frac 1 n & , & Else\end{matrix} \right. Fertig\) |