| x | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
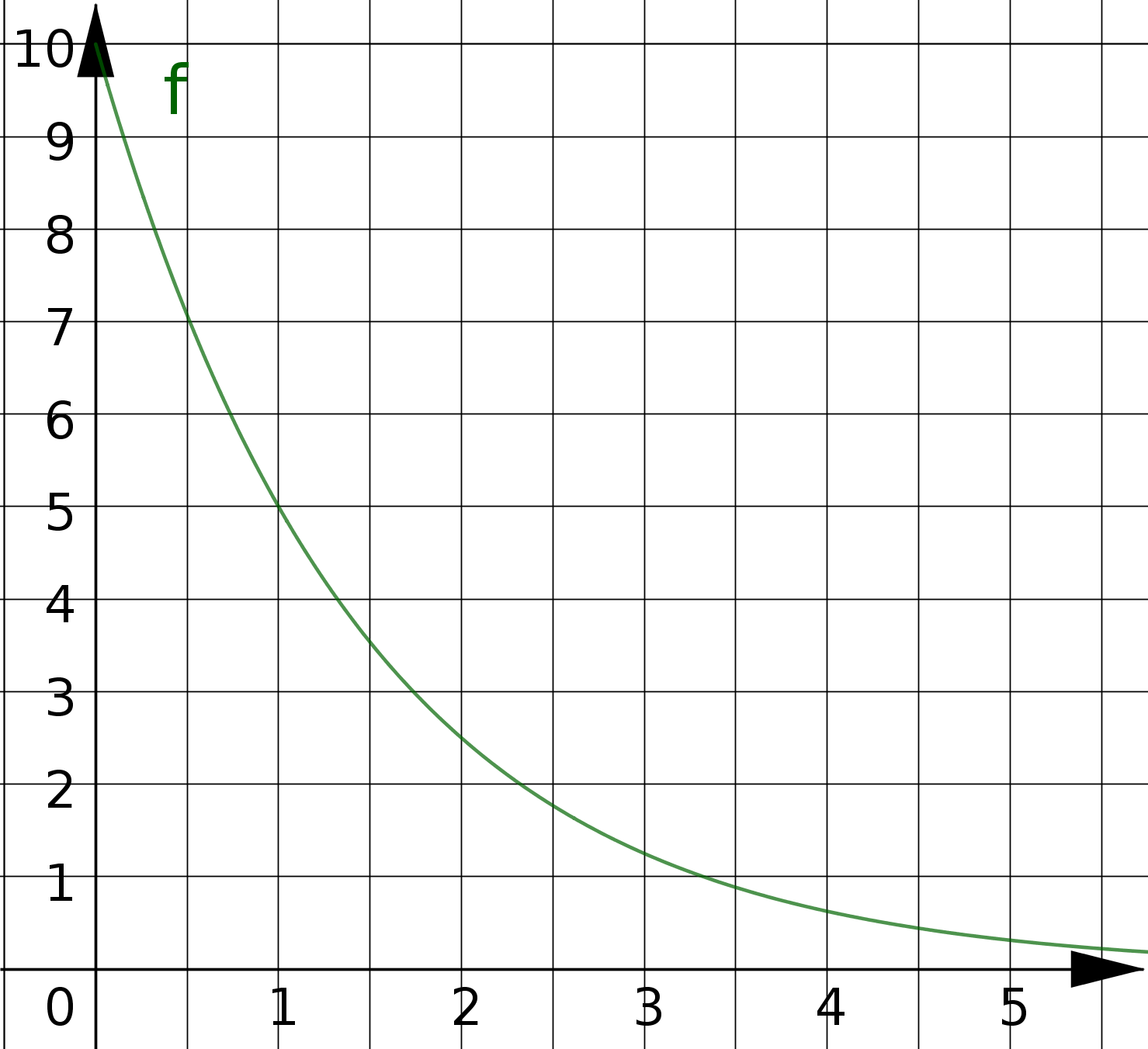
| \[f(x)\] | 10 | 5 | 2,5 | 1,25 |
Beim Thema Grenzprozesse geht es darum, Kategorien zu finden, wie sich Prozesse
verhalten, wenn sie sich einer Grenze nähern. Viele Beispiele dafür kennen wir
vom Wachstum z.B.:
10 mg radioaktives Fluor zerfällt mit einer Halbwertszeit von
einer Sekunde.
| Funktionsgleichung | Wertetabelle | Funktionsgraph | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \[f(x)=10 \cdot \left(\frac{1}{2}\right)^x\] |
|
 |